Appendix 1 - Calculations regarding Śaka and Jupiter (Bṛhaspati)

Note: This appendix is extract from chapter eight of the Bṛhat-saṃhita verses 20-22.

[Note We will now explain the principles involved in the calculations contained in the three preceding stanzas: A kalpa contains 1000, Catur Yugas, in a kalpa, according to Āryabhaṭṭa the number of sidereal revolutions of years of the Sun is 4320000000; and the number of sidereal revolutions of Jupiter is 364224000; but as each revolution contains 12 years, the number of Jupiter’s years in the same period is 437,0688,000, in other words, in a Catur yuga.

No. of Solar years : No. Jupiter’s years
                             :: 43,20,000: 43,70688:: 1875: 1897
                         or:: 3750: 3794, to suit ourselves to the figures in the text. So that for every 3,750 solar years we get 3,750+44 years of Jupiter; therefore a solar year =

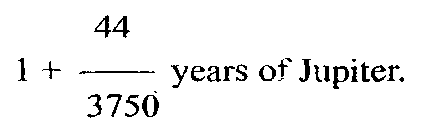
We will now find out the number of years by which Jupiter had advanced in the Kaliyuga at the commencement of the Śaka era, it being known that the number of solar years during the said period is 3179. We have the following proportion, 3750: 3794:: 3179: x, years of Jupiter required.

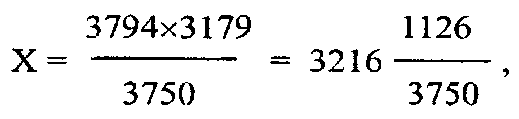
the number of years of Jupiter from the commencement of the Kaliyuga to the commencement of the Śaka era.

Now it is known that Kaliyuga commenced in the year Vijaya (the 27^th year from Prabhava, which is the first year in a cycle of 60 years of jupiter).

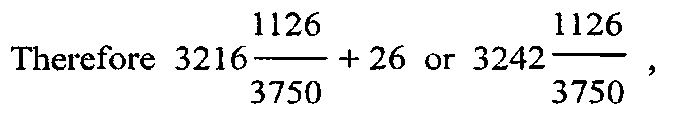
being divided by 60, the remainder will give the particular year of Jupiter (in his cycle of 60 years) from Prabhava at the time of the commencement of the Śaka era and this remainder is

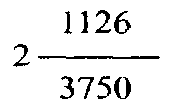
which is the 3^rd year or the year Śukla of the cycle.

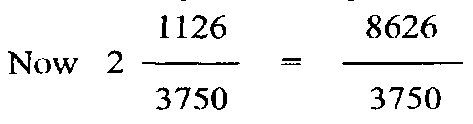
Coming down to the period subsequent to the commencement of the Śaka era we have, as already stated,

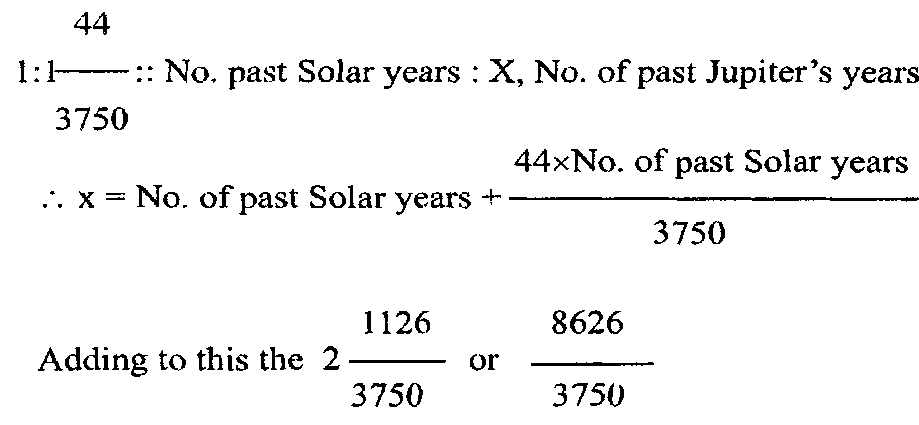
years which elapsed from the beginning of Prabhava to the time of the commencement of the Śaka era we get,

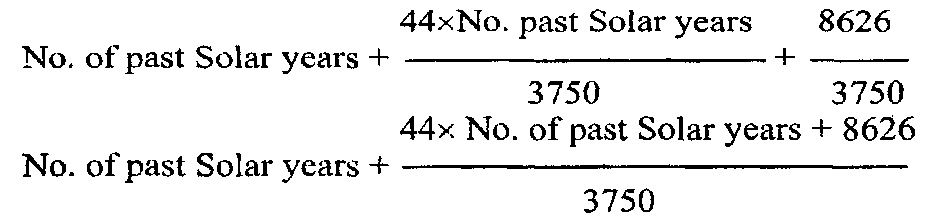
when this is divided by 60 the remainder will give the year of Jupiter in his cycle of 60 years commencing from Prabhava; call this remainder J.

Now as there are 12 yugas (each of 5 years) in a cycle of 60 years J being divided by 5, the quotient will give the number of yugas that have elapsed from the first yuga of Viṣṇu and the remainder the number of years by which Jupiter has advanced in the current yuga (For the names of these yugas vide stanza 23).

This brings us to the end of Stanza 21. Stanza 22 aims at discovering the particular lunar mansion or Nakṣatra in which Jupiter might happen to be at any given time: Time taken by Mean Jupiter to go over a sign of Zodiac is called a year of Jupiter.

Therefore a number of such years will represent the number of signs gone over by Mean Jupiter during the time. In 12 such years Mean Jupiter makes a circuit of the heavens. Now the year Prabhava commences when Jupiter enters (or reappears according to commentator) in the constellation of Dhaniṣṭhā in the month of Maghā, and Mean Jupiter takes 12 years from Dhaniṣṭhā to it again. If therefore J were divided by 12, the remainder will show the number of years taken by Mean Jupiter to go over the number of lunar mansions lying between Dhaniṣṭhā and the particular lunar mansion in which Jupiter might happen to be at the given time. Call this remainder R. As stated above, R, which represents the number of years, also represents the number of Zodiacal signs. Now as each sign contains 24 lunar mansions the number of lunar mansions required (from Dhaniṣṭhā) = 2¼ x R = 9/4 R. This brings us to the end of Stanza 22.

It will be observed from the above that the figure given in stanza 20 is 8589 and not 8626. The fact is that in our process we adopted Āryabhaṭṭa’s figure, there being a difference of opinion among Hindu Astronomers regarding the number of the sidereal revolutions of Jupiter in a kalpa. For instance: Bhāskarācārya gives it as 364 226 455 against 364 224 000 of Āryabhaṭṭa. But what we want is Varāha-Mihira’s figure. As his Astronomical work, Pañcasiddhāntikā, is now lost we cannot give it exactly; but calculating backwards from the figure 8589 appearing in the text, we find the number of sidereal revolutions of Jupiter, according to Varāha-Mihira to be 364 190 000. This is probably the correct figure.]